Hvor langt unna kan du se en meteor?
>Jeg får e -post.
De fleste stiller spørsmål av forskjellige typer, hvorav de fleste er ganske enkle å svare på (faktisk kan mye besvares ved å google, hint hint). Men noen ganger får jeg et spørsmål som er vanskeligere å svare på, eller til og med et som jeg har lurt på om meg selv, men aldri har klart å finne ut.
Så jeg var ganske fascinert da jeg fikk et spørsmål fra Bad Reader Dean Lewis om meteorer. Under Perseid meteorregn i 2018 var han borte fra familien, atskilt med omtrent 1000 kilometer. Hvis han så en meteor, var det mulig at de kunne se den samme fra deres mer fjerne område?
Det korte svaret er: Ja! Det lange svaret er ... matematikk. Kul, morsom matte.
Og ettersom hvordan den årlige Geminid -meteordusjen i 2018 når denne artikkelen blir lagt ut i kveld, synes jeg det er på sin plass å finne ut av dette.
Crash Course Astronomy: Meteorer, Meteoroids, and Meteorites, Oh My!
Hvis jorden var helt flat, så kunne du i prinsippet se en meteor helt til hvilken som helst kant av jorden. Så lenge du er over bakken, til og med en liten bit, når siktelinjen din hver kvadratcentimeter av planeten på din side, så hver meteor er synlig for alle. I virkeligheten er luften ikke helt gjennomsiktig, så på en avstand ser du gjennom så mye dritt at du ikke kan se noe.
Jorden er imidlertid ikke flat. Alvor! Det er rundt. Og atmosfæren omgir den som et skall, blir tynnere med høyden og til slutt petering ut; at høyden avhenger av definisjonen din av plass. Imidlertid kan vi jukse litt siden vi kan vitenskap: Meteorer som dem i dusjer har en tendens til å brenne opp rundt 100 kilometer over bakken. Den høyden avhenger av mange ting, inkludert hvor stor meteoroider (de solide bitene av interplanetarisk rusk som glir gjennom rommet) er, hvor raskt de beveger seg, i hvilken vinkel de kommer inn i atmosfæren, og så videre. Men la oss kalle det 100 km.
hvorfor er maisbarn vurdert til r
Det nærmeste en meteor kan være deg er hvis du er rett under den, og så er det 100 km rett opp (på høyden). Hvis det brenner opp lenger vekk fra zenitten, må det være lenger fra deg. Lengst unna kan du se en meteor, det er fornuftig, er derfor hvis det er akkurat i horisonten.
Geometrien til den ser slik ut (merk: IKKE i målestokk):
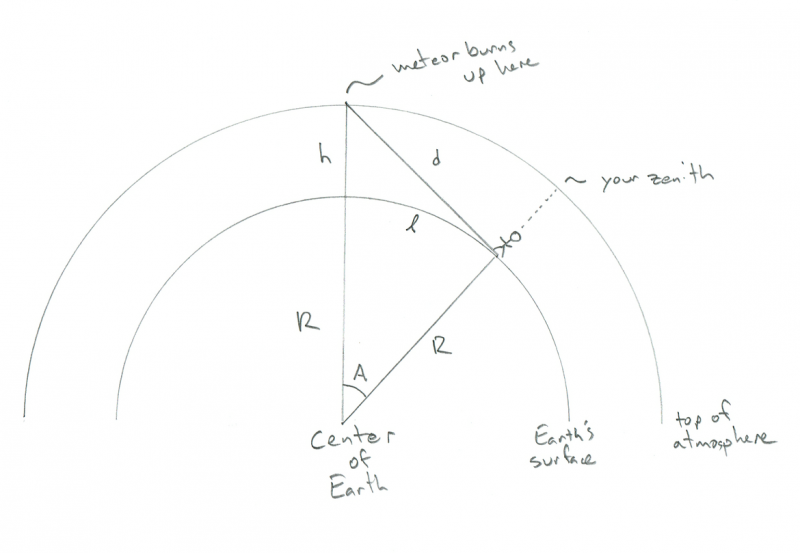
Skjematisk viser geometrien til en observatør som ser på en meteor som brenner opp. Kreditt: Phil Plait
Du kan se den lille pinnefiguren som står på overflaten av den buede jorden - la oss si at det er deg - med (også buet) atmosfære over seg. I dette diagrammet er R jordens radius (6,4000 km), h er høyden meteoren brenner opp (100 km), og d er avstanden fra deg til meteoren. A er vinkelen mellom posisjonen din på jorden og meteorens posisjon over den, og kursiv l (som i lengden) er avstanden du må gå for å få meteoren til å være direkte overhead (jeg vet at det virker som en merkelig ting å ville vite, men tål med meg). Merkelig kan du beregne alt du trenger her uten å vite d, men jammen er det kult å vite hvor langt unna meteoren er, ikke sant?
Nøkkelen til alt dette er å se at vinkelen mellom meteoren, deg og jordens sentrum er en rett vinkel. Det er fordi meteoren er i horisonten sett av deg (eller, hvis du foretrekker morsom sjargong, på tangentlinjen på den indre sirkelen der R skjærer den). Det gjør trekanten til en rett trekant, og hvis du husker videregående matematikk, betyr det at du kan finne alle sider og vinkler!
Huske pythagorasetningen ? I en høyre trekant er kvadratet av lengden på hypotenusen lik summen av kvadratene på de to andre sidene*. I trekanten vår er hypotenusen R+h, og de andre sidene er R og d.
Så
(R+t)2= d2+ R2
eller multiplisere på venstre side (bruk FOLIE ):
R2+ 2Rh + h2 = d2+ R2
Løs for d for å se hvor langt unna meteoren er fra deg. Vær oppmerksom på at R2 er på begge sider, så avbryt dem for å få
d2= 2Rh + t2
vurdering av fantastiske dyr og hvor du finner dem
Eller
d = kvadratrot (2Rh + h2)
Vi kjenner alle disse tallene! Plug-n-chug, baby:
d = kvadratrot (2 x 6400 x 100 + 10.000) = 1.136 km
Aha! Dette betyr at hvis du ser en meteor i horisonten, er den over 1100 kilometer unna! Det er langt, og teknisk sett lengst unna kan du se en meteor fra bakken.
La oss nå finne kursiv l. Først må vi kjenne vinkelen A. Det krever litt trigonometri. Det er mange trig -identiteter du kan bruke til å finne ut av dette, men min favoritt†er at i en rett trekant er sinus for en vinkel lengden på den motsatte siden dividert med lengden på hypotenusen. Så hvis vi får det forholdet, kan vi ta den inverse sinus (eller arcsine) for å få vinkelen.
sin (A) = d / (R + h)
så
A = uten-1(d / R + t)
Plug-n-chug igjen, og jeg får A = 10 °. Det er en anstendig del av jordoverflaten!
savner han meg uten kontakt
Og nå kan vi få kursiv l. Det er 360 ° rundt jorden, og jordens omkrets er 2 x pi x radius = 40 192 km, så det er
40.192 km / 360 ° = 112 kilometer per grad
som igjen betyr 10 ° = 1120 kilometer. Det er ganske nær d, noe som ikke er så overraskende. Tegningene er overdrevne, men i virkeligheten er luftskallet over oss lite sammenlignet med størrelsen på jorden. Hvis jeg laget tegningene i målestokk, ville du se at d og l virkelig er ganske lange.
OK, så hvorfor er jeg het og plaget av å finne l? På grunn av det opprinnelige spørsmålet! Hvis du glemte tross alt matematikken, er det hvor langt unna to mennesker kan være og fremdeles se den samme meteoren?
Vel, i så fall ville meteoren være direkte mellom dem og på hver sin horisont. Den geometrien ser slik ut:
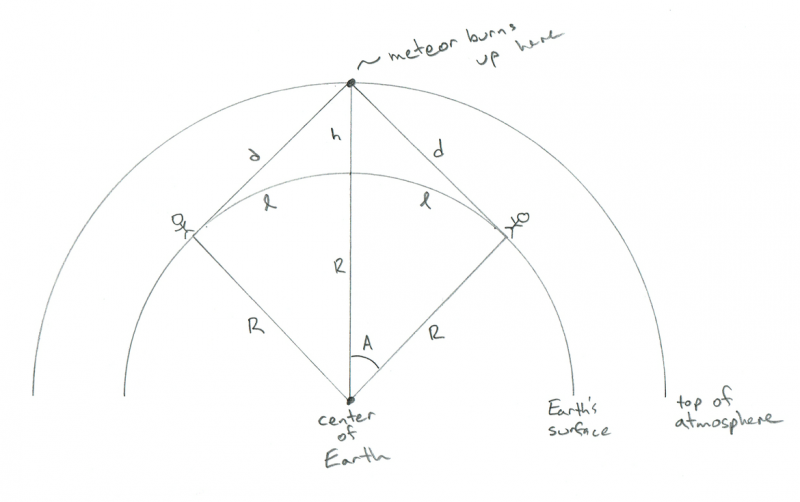
Skjematisk viser geometrien til to observatører som ser på en meteor som brenner opp nøyaktig mellom dem. Kreditt: Phil Plait
AHA! Nå skjønner du hvorfor jeg vil ha l! Avstanden mellom de to personene er bare 2 x l! Så nå har vi svaret:
For at to mennesker skal se den samme meteoren, kan de ikke være mer enn 2 x 1120 = 2240 kilometer fra hverandre. Som et eksempel er det ganske nær avstanden mellom Washington, DC og Denver. Wow.
dårlige tider i el royale sunn fornuft media
Forresten, for en endring av perspektiv (bokstavelig talt) betyr dette fra meteorens synspunkt at den kan se en strekning av jorden 2 240 kilometer bred (som i, DC på den østlige lemmen på jorden og Denver på den vestlige). Det er ganske kult.
Og det bringer oss til det faktiske svaret på Dean's spørsmål: Hvis han var 1000 km fra familien, så ja, teknisk sett kunne de se den samme meteoren. Hva med det?
Nå antar dette igjen at luften er helt klar og alt det, som i virkeligheten er praktisk talt umulig. Så denne matematikken representerer en ideell situasjon (inkludert ideen om at meteoren er nøyaktig mellom dem).
La oss være mer realistiske. La oss si at meteoren brenner opp på himmelen i en høyde av 45 ° over horisonten for begge observatørene. Hvor langt unna ville de være fra hverandre? Vel, igjen, forutsatt at meteoren er nøyaktig mellom dem, er geometrien mer slik:
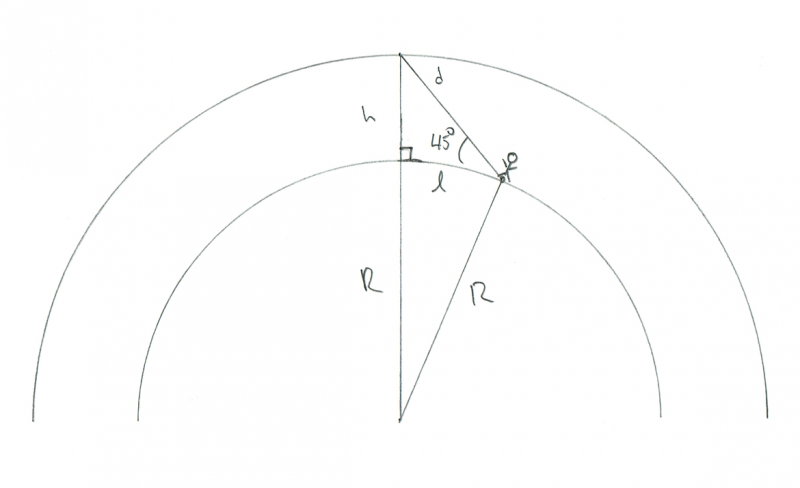
Skjematisk viser geometrien til en observatør som ser en meteor som brenner opp 45 ° over horisonten. Kreditt: Phil Plait
Dette er faktisk vanskeligere å løse, men jeg vet et annet triks: Hvis vi antar at l er liten, vil ikke jordens krumning være viktig. For eksempel, hvis jeg vil vite avstanden mellom to trær i hagen min, bryr jeg meg ikke om at jorden er buet. På en så liten avstand kan jeg anta at den er flat. La oss gjøre den antagelsen her.
I så fall har vi en annen rett trekant, men denne gangen er den rette vinkelen den under meteoren. Jeg merket det til og med i diagrammet med den lille firkantede notasjonen. Så hvis det er en 90 ° vinkel, og vinkelen vår til meteoren er 45 °, så er den siste vinkelen (fra meteoren til observatøren) også 45 °. Det betyr at dette må være en likebent trekant, så l og h er like! Siden vi vet at h er 100 km så må l.
Og det betyr at avstanden mellom våre to observatører er det dobbelte, eller 200 km.
Forresten, i dette tilfellet er avstanden til meteoren omtrent 141 km. Jeg overlater å bekrefte det som en øvelse til leseren.
I prinsippet betyr dette at hvis du vet hvor høyt utenfor horisonten en meteor er, og høyden den brant opp i, kan du beregne avstanden (eller hvis du vet avstanden, kan du få dens høyde). Triggen er ganske komplisert, og jeg tror jeg har kastet nok matte på deg i dag.
Men det er kult å tenke på at litt matematikk fra videregående skole kan ha en så morsom applikasjon. Og jeg skal innrømme at det er poetisk og romantisk å vite at så lenge separasjonen ikke er for langt, er det mulig å dele å se et stjerneskudd med noen andre. For en herlig tanke.
* I Trollmannen fra Oz , fugleskremselen tok dette feil etter han har en hjerne.
† Av kurs Jeg har en favoritt trig -identitet. Hva er ditt?